
İçindekiler
Yörünge Mekaniğinin Gizli Tarihi: Brahe, Kepler ve Mars
İnanılması güç olsa da Brahe ve Kepler birlikte sulh içinde çalışırken…
Hiç konuk olduğunuz bir evde tuvalete gitmek için izin istemeye utandığınız ve masadan kalkamayıp kıvrandığınız bir an oldu mu? Katıldığı şölende kendini benzer bir durumda bulan bir Danimarka asilzadesi eğer kibarlığı bir kenara bırakıp tuvalete gitseydi, astronomi ve yörünge mekaniğinin tarihi çok farklı bir şekilde yazılabilirdi. Gökbilimci Tycho Brahe’nin şölenden on bir gün sonra, 24 Ekim 1601’de, böbrek yetmezliği nedeniyle hayata gözlerini yumarken arkasında bıraktığı en değerli miras, teleskop kullanmadan gerçekleştirdiği, son derece hassas astronomik gözlemlerdi. Bu ani ölüm, özellikle, gökyüzündeki hareketine kimsenin akıl sır erdiremediği Mars’la ilgili gözlemlerine bir süredir devam eden 30 yaşındaki asistanı Johannes Kepler için büyük bir fırsat demekti. Gözlemlerin paragöz varislerin eline geçmesinden korkan Kepler olan biteni birkaç yıl sonra bir mektupta şöyle açıklayacaktı: “İtiraf etmeliyim ki Tycho hayatını kaybettiğinde varislerinin yokluğundan ya da dikkatsizliğinden istifade etmekte gecikmedim ve gözlemleri kanatlarımın altına aldım, belki de gasp ettim.”
Brahe’nin gözlemlerini kullanarak Mars’ın hareketinin şifrelerini sekiz günde çözeceğini iddia eden Kepler’in ilk sonuçlarını yayımlaması ancak sekiz yıl sonra mümkün olabildi. 1609’da yayımlanan Astronomia Nova adlı eserinde bugün Kepler yasaları olarak bildiğimiz bağıntıların ilk ikisi yayınlandı.
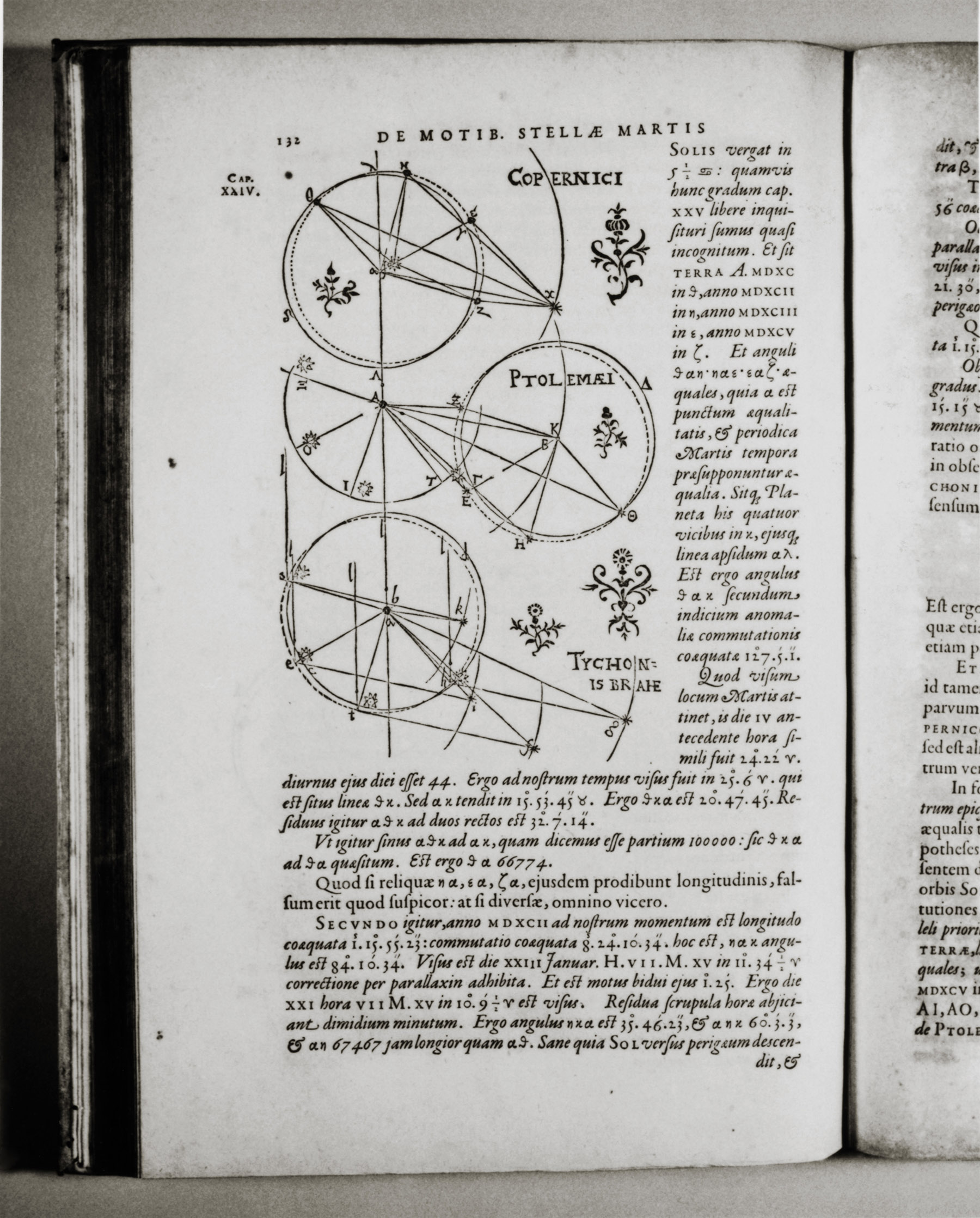
Kepler’in eserinden bir sayfa
Kepler’in Birinci Yasası
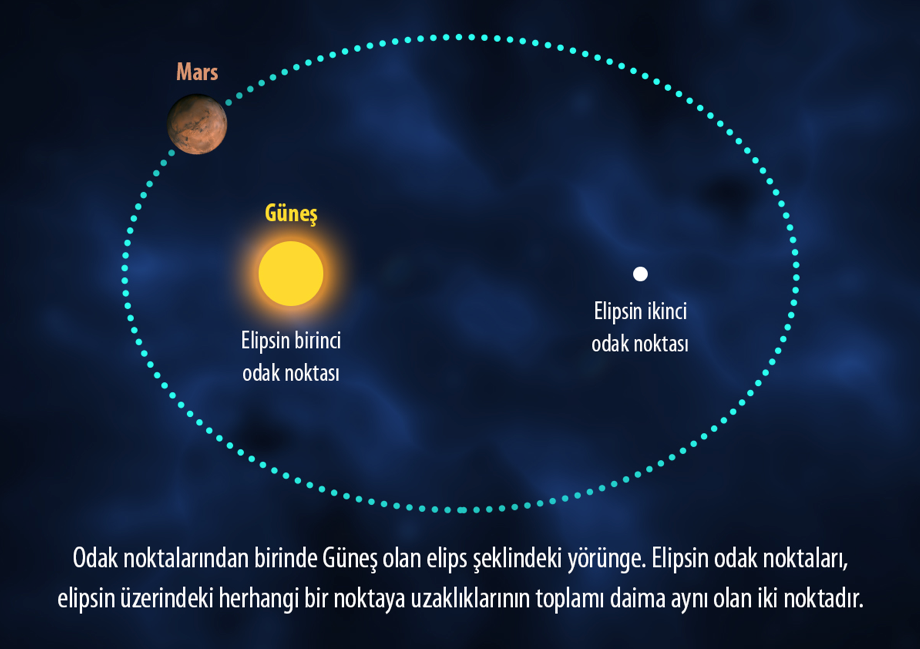
Mars ve diğer tüm gezegenler, odak noktalarından birinde Güneş’in olduğu elips şeklindeki bir yörüngede hareket eder.
Kepler’in İkinci Yasası
Güneş ile Mars’ı veya herhangi bir gezegeni birleştiren çizgi eşit zamanda eşit alanları tarar.

Kepler’in ikinci yasası
Bugün bize son derece basit gelen bu iki yasa, merkezinde Güneş’in olduğu, Dünya’nın ve diğer gezegenlerin Güneş’in etrafında hareket ettiği Kopernik sisteminden bile daha ileriydi. Zira Kopernik gezegenlerin dairesel yörüngelerde sabit bir açısal hızda hareket ettiğini savunuyordu. Bu eksiklikleri nedeniyle de özellikle Mars’ın yörünge hareketindeki anormallikleri açıklayamıyor ve çokça eleştiriliyordu. Oysa Kepler hem gezegenlerin yörüngelerinin mükemmel bir çember şeklinde olmadığını hem de açısal hızlarının değişken olduğunu gösteren basit bir bağıntı ile Mars’ın belirli bir zamanda gökyüzünde nerede olacağını çok daha doğru bir şekilde tahmin edebiliyordu.
Tam bu noktada duralım ve Mars’ın neden o zamana kadarki tüm gökbilimcilerde kafa karışıklığına yol açtığını anlamaya çalışalım.
Tüm gezegenler Kepler’in de keşfettiği gibi elips şeklindeki yörüngelerde hareket eder. Ancak elipsin mükemmel bir çemberden ne kadar farklı olduğu basıklık adı verilen bir değişken ile tanımlanır. Basıklığın 0 olması elipsin özel bir durumu olarak tanımlanabilecek çembere karşılık gelir. Basıklık değeri 1’e doğru yaklaştıkça yörünge daha eliptik bir hâle gelir ve 1’e eşit olduğunda “koparak” bir parabol şeklini alır.

Yukarıdaki çizimde farklı basıklık değerlerine sahip yörünge şekilleri görülüyor.
O dönemde bilinen gezegenlerden Satürn için basıklık değeri 0,054 ve Jüpiter için 0,048. Dünya’nın basıklık değeri ise bunlardan da küçük: 0,016. Diğer bir deyişle yörüngemiz mükemmel bir çembere o kadar yakın ki Güneş’e yaklaşıp uzaklaştığımızı pek fark edemiyoruz. Mars’ın basıklık değeri ise 0,093, yani Dünya’nınkinin altı, Jüpiter’inkinin iki katı.
Kepler’in ikinci yasasına göre gezegenler sabit bir açısal hızda hareket etmek yerine Güneş’ten uzaklaştıkça yavaşlıyor ve Güneş’e yaklaştıkça hızlanıyor. Dolayısıyla görece yüksek basıklık değerine sahip olan Mars gökyüzünde beklediğimiz konumda değil, zaman zaman daha ileride zaman zaman da daha geride görülüyor. Kepler’e dek gökbilimcilerin çözemediği muamma tam da buydu.
Kepler 1619 yılında çıkardığı Harmonices Mundi adlı kitabında bugünKepler’in üçüncü yasası olarak adlandırdığımız bağıntıyı ortaya koydu: Bir gezegenin Güneş etrafında bir turunu tamamlama süresi yani periyodun (P) karesi, Güneş’e olan ortalama mesafesinin yani yarısal eksenin (a) küpüyle orantılıdır.
Diğer bir deyişle:
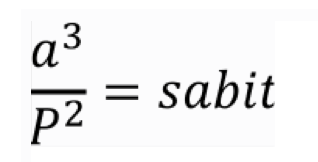
Kepler Güneş’in kütlesini (M), Dünya’nın kütlesini (m) ve evrensel kütleçekim sabitini (G) bilseydi şu denklemi yazabilecekti:
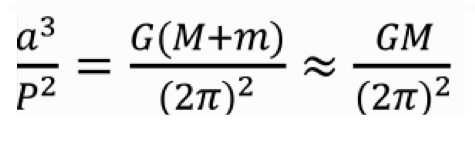
Keplerin ilk kez ortaya koyduğu bu bağıntı bütün gezegenler için geçerliydi. Dolayısıyla Kepler bir anlamda Güneş Sistemi için geçerli olan “çekim sabitini” keşfetmişti.

Harmonices Mundi
Kepler bugün kendisinin adıyla andığımız “gezegen hareket yasaları”nı yayımladığında gezegenlerin hareketini o güne dek görülmemiş bir doğrulukta tanımlamayı ve tahmin etmeyi başardı. Kepler, gezegenlerin yörünge hareketinin “nasıl” olduğunu tarif edebiliyor ancak bu hareketin “sebebini” tam olarak anlayamıyordu. Güneş Sistemi’ndeki gökcisimlerinin Güneş tarafından uygulanan bir tür itme kuvveti ile belirli bir yörüngede ilerlediğini düşünüyordu. Ama bu kuvveti, diğer bir deyişle gökcisimlerinin “neden” belirli bir yörüngede hareket ettiğini açıklamak için Astronmia Nova‘nın yayımlanmasından yaklaşık 25 yıl sonra doğacak olan Isaac Newton’un bilim sahnesine çıkışını beklemek gerekecekti.
