İçindekiler
Meşhur Denklemler
Denklem, özdeşlik, bağıntı ve formül; matematik derslerinden de aşina olduğumuz terimler.
Bu terimlerin Türk Dil Kurumu sözlüğündeki karşılıkları şu şeklide:
Denklem: “İçinde yer alan bazı niceliklere ancak uygun bir değer verildiği zaman sağlanabilen eşitlik.”
Özdeşlik: “İki yanı birbirinin aynı olan veya harflerle verilen sayısal değerler ne olursa olsun iki yanı da sayıca eşit değerler alan eşitlik.”
Bağıntı: “İki veya daha çok nitelik arasında matematik işlemleri yardımı ile kurulan bağlılık veya eşitlik.”
Formül: “Bir veya birçok niceliğe bağlı bulunan bir niceliğin hesaplanmasına yarayan matematiksel anlatım.”
Aslında bu matematiksel cümlelerin hepsi eşitliği belirtir yani “=” işaretinin sağında ve solunda yer alan ifadelerin birbirine eşit olduğunu söyler. Günlük dilde genelde denklem hepsini kapsayacak şekilde kullanılır.
Bu terimler arasındaki ayrımın üzerinde çok durmadan “meşhur” denklem örneklerimize geçelim.
T
Rivayete göre, ünlü matematikçi Gauss (1777-1855) öğrenciyken matematik öğretmeni sınıfa bir soru yöneltir: “1’den 100’e kadar olan doğal sayıların toplamı kaçtır?”. Öğrencilerin bu soru üzerinde epey zaman harcayacağını düşünen öğretmen, birkaç dakika sonra Gauss’un defterine hiçbir işlem yapmadan doğru sonuç olan 5050 sayısını yazmış olduğunu görür. Peki Gauss bu işlemi zihinden nasıl yapmıştır?
Gauss’un yöntemini bir örnek ile açıklayalım. 1’den 8’e kadar olan sayıların toplamı T olsun. T değerini hesaplamaya çalışalım. Toplamı aşağıdaki gibi artan sırada yazdıktan sonra alt satıra aynı toplamı bu defa azalan sırada yazalım. Bu iki satırdaki terimleri alt alta toplayalım:
Burada bulmak istediğimiz toplamın iki katını elde ettik.
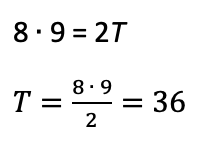
Günümüzde 1’den n‘ye kadar ardışık doğal sayıların toplamını bulmak için kullandığımız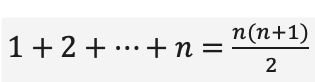
formülünün doğruluğunu Gauss’un yöntemini kullanarak ispatlayabiliriz.
Yine terimleri artan ve azalan sırada alt alta yazıp toplarsak bu defa alt alta gelen terimlerin toplamı n + 1, topladığımız ikililerin sayısı ise n olacak. Buradan
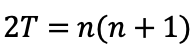
ve
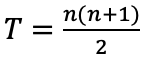
eşitliğini elde ederiz.
Gauss’un yöntemi kullanılarak başka toplamlar da hesaplanabilir. Örneğin ilk 8 tek sayının (yani 1’den 15’e kadar tek sayıların) toplamını bulmayı deneyin. Peki ntane tek sayının toplamını veren formülü bu yöntemle elde edebilir misiniz?
Pisagor Bağıntısı
‘
a2+ =
Bu ilişki aslında Pisagor’dan çok önce, Mısırlılar ve Babilliler tarafından biliniyor ve çeşitli hesaplamalarda kullanılıyordu. Bu bağıntıyı sağlayan özel üçlülerin listelerini çıkarmışlardı (örneğin 3-4-5 ve 5-12-13). Hatta Mısırlıların piramitlerin inşasında bazı özel üçlülerden faydalandığı düşünülüyor.
Daha önceki medeniyetler, matematiksel özellikleri genelleme ihtiyacı hissetmemiştir. Genelleme ve ispat, Antik Yunan medeniyetinin matematiğe en büyük katkılarındandır.
Bu bağıntının farklı alanlardaki uygulamaları dışında başka bir önemi de irrasyonel sayıların keşfine kapı aralamasıdır. Bağıntının tüm dik üçgenler için doğru olduğunun ispatlanması ile ortaya çıkan problem, dik kenar uzunlukları 1’er birim olan bir dik üçgenin hipotenüs uzunluğunun ne olacağıydı.Bağıntıya göre 12+ 12= c2yani karesi 2 olanbir sayı! Fakat Pisagor ve takipçilerinin düşüncesine göre her şey tam sayı veya iki tam sayının oranı ile açıklanabiliyordu.
Günümüzde karesi 2 olan sayıyı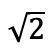 
ile gösteriyoruz ve bu sayının iki tam sayının oranı olarak yazılamayacağını yani rasyonel bir sayı olmadığını biliyoruz.
Goldbach Hipotezi
Şimdi bahsedeceğimiz bağıntının meşhur olmasının sebebi diğerlerinden biraz daha farklı. Henüz doğruluğu ispatlanamadı yani bu bir iddia. Christian Goldbach isimli bir matematikçi, 1742’de ünlü matematikçi Leonhard Euler‘e bir mektup yazarak doğru olduğunu düşündüğü bir bağıntıdan bahsetmiştir. Euler de Goldbach’ın iddiasına denk olan başka bir bağıntı öne sürmüş ama bir ispat sunamamıştır.
İddia şöyle: “2’den büyük her çift sayı iki asal sayının toplamı olarak yazılabilir.”
Deneyelim:
Tabii ki bir matematikçi beş tane çift sayı için eşitlik sağlanıyor diye bu özelliği tüm çift sayılara genelleyemez. İddianın doğru olduğunu göstermek için matematiksel bir ispat yapması gerekir. Eğer tüm çift sayılar için bu eşitlik doğru değilse iddiayı çürütmek için iki asal sayının toplamı şeklinde yazılamayan, 2’den büyük bir çift sayı bulmak gerekir. Teknolojinin de yardımı ile 400.000.000.000.000 sayısına kadar deneme yapıldı ancak eşitliği sağlamayan bir çift sayı bulunamadı. Henüz kanıtlanamadığı için bu iddia hipotez (varsayım) olarak adlandırılıyor.
Euler Özdeşliği
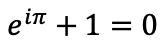
Bu denklemin matematiğin en güzel denklemlerinden biri olduğu söylenir. Bunun sebebi, matematikte kullanılan en temel beş sabiti bir araya getiren sade ve şaşırtıcı bir eşitlik olmasıdır. Peki nedir bu beş sabit? 1 ve 0’ı zaten biliyoruz.
e
i
?
Pozitif bir sayı olan e’nin bir kuvveti alınıp 1 eklenince sonucun 0 çıkması ayrıca şaşırtıcıdır.
Peki bu sayılar nasıl bir araya geldi? Her şey Euler’in exüstel fonksiyonu ile sin(x)ve cos(x)trigonometrik fonksiyonları arasında bir ilişki keşfetmesi ile başladı. Bu üç fonksiyonun seri açılımları birbirine benziyordu ama üçünü bir araya getirebilmek için i sayısını da işin içine katmak gerekti.
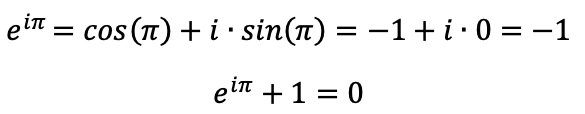
Bu keşfin matematiğin farklı dallarını ilgilendiren uygulamalara etkisi oldu.
Bu yazıda matematikteki bazı meşhur denklemlerden bahsettik. Tabii meşhur denklem deyince doğa bilimleri ve sosyal bilimler gibi farklı bilim dallarında ortaya konulmuş daha birçok denklem akla geliyor. Bunlardan biri de görelilik kuramını ortaya atan fizikçi Albert Einstein’ın e = mc2denklemi. Bu denklem cismin kültesi (m) ile enerjisi (e) arasındaki ilişkiyi ortaya koyar. Denklemdeki c ise ışık hızını temsil eder.
Bu tür denklemlerin doğruluğunu kanıtlamak için matematiksel özellikler ve çıkarım kuralları yeterli değildir. İlgili alanın kuramları ve varsayımları kullanılarak gözlem ve deneye dayalı çıkarımlarda bulunulur ve değişkenler arasındaki ilişkileri açıklayan denklemler elde edilir.
- Mackenzie, D., 24 Denklemde Matematiğin Hikayesi, Ketebe Kitap ve Dergi Yayıncılığı, İstanbul, 2018.
- https://artofproblemsolving.com/wiki/index.php/Goldbach_Conjecture