
Astronomiden Matematiğe
2019 yılı Prof. Dr. Fuat Sezgin Yılı olarak ilan edildi. 2019 yılı boyunca Prof. Dr. Fuat Sezgin’in İslam bilim ve teknoloji tarihine katkılarını farklı yazılarla ele alacağız. Prof. Dr. Fuat Sezgin anısına hazırladığımız diğer yazılara ulaşmak için tıklayın.
Trigonometri lisede matematik dersinde karşılaştığınız ve belki de anlamakta zorlandığınız konulardan biri. Dik üçgenlerin iç açıları ve kenar uzunlukları arasındaki bağlantılarla ilgili matematiğin bu dalı size soyut gelebilir. Geçmişte insanlar denizcilikte, haritacılıkta ve astronomi yani gökbilimde karşılaştıkları problemleri çözmek için trigonometriden faydalandı. Günümüzde de trigonometri günlük hayatta karşılaştığımız farklı problemleri çözmek için kullandığımız yöntemlerden biri.
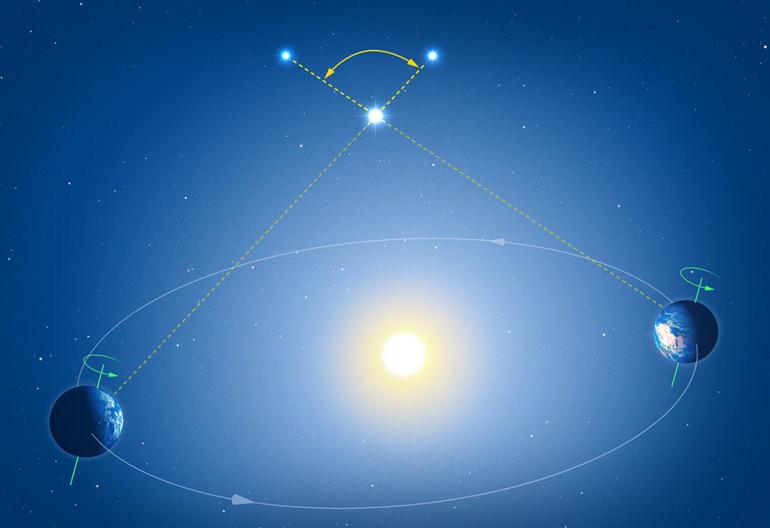
Örneğin paralaks, uzaydaki gökcisimlerinin Dünya’dan uzaklıklarını belirlemek için kullanılan matematiksel bir yöntemdir.
İnsanlar Güneş’in ve gökyüzündeki diğer gökcisimlerinin hareketlerini çok eski zamanlardan beri gözlüyordu. Yüzyıllarca süren gözlemlerden sonra gökcisimlerinin (örneğin Güneş’in, Ay’ın, o zaman bilinen gezegenlerin, takımyıldızların ve yıldızların) hareketlerinin belirli bir düzen içinde tekrar ettiğini fark eden bilginler bu astronomik olayların zamanını tahmin edebilmek için tablolar oluşturdu. Bu amaçla üçgenlerin kenar uzunlukları ve iç açıları arasındaki ilişkilerden yararlandılar.
8. yüzyılda Bağdat’ta kurulan Beyt’ül-Hikme’de (Bilgelik Evi) Yunan, Hint, Mısırlı, Babilli, Çinli bilginler -örneğin Aristoteles, Arşimet, Platon, Öklit- tarafından yazılan kitaplar Arapçaya çevrilerek burada dünyanın en önemli bilgi koleksiyonlarından biri oluşturuldu. Milattan sonra ikinci yüzyılda İskenderiye’de yaşayan matematikçi ve gökbilimci Ptoleme’nin (Batlamyus olarak da bilinir) gökcisimlerinin hareketini matematiksel kavramlarla açıkladığı Almagest isimli eseri de Macisti (En Büyük) ismiyle Arapçaya çevrilmişti.

Tarihin en önemli araştırma merkezlerinden biri olan Beyt’ül-Hikme’nin bir çizimi
Prof. Dr. Fuat Sezgin, İslam Uygarlığında Astronomi, Coğrafya ve Denizcilik kitabında, Müslüman bilgilerin bu kitapları sadece tercüme etmediklerini aynı zamanda düzeltmeler ve eklemeler yaparak geliştirdiklerini belirtiyor. Örneğin Halife el-Me’mun, Yahya b. Ebu Mansur isimli gökbilimciye Ptoleme’nin Çizelgeler El Kitabı‘ndaki verileri ve gözlemleri kontrol etme görevini vermişti. Yapılan araştırmalar Ebu Mansur’un Güneş ve Ay tutulmalarının zamanını belirlemede Ptoleme tarafından kullanılmayan farklı bir yöntem kullandığını gösteriyor.
Ptoleme’nin Almagest kitabındaki “Dairedeki Kirişler Tablosu”nda, yarıçapı 60 birim olan bir dairede, 0 ve 180 derece arasında yarım derecelik aralıklarla değişen merkez açının karşısında bulunan kiriş uzunluklarına yer verilmişti. Bu değerler 1/4 ile 90 derece arasındaki açıların sinüsüne denk geliyordu.
Bugün kullandığımız sinüs (bir dik üçgende bir açının karşısındaki kenarın uzunluğunun hipotenüsün uzunluğuna bölünmesiyle elde edilen oran, açının sinüsü olarak ifade edilir) ve kosinüs (bir dik üçgende bir açının komşusundaki kenarın uzunluğunun hipotenüsün uzunluğuna bölünmesiyle elde edilen oran, açının kosinüsü olarak ifade edilir) değerlerine ait tablolara Hintlerin kitaplarında rastlanıyordu.
O dönemlerde gökbilimciler sinüs ve kosinüs fonksiyonlarını gökbilimle ilgili problemlere çözüm bulmak için kullanıyordu.

Gökbilimciler, gökcisimlerinin konumlarını ve hareketlerini gök küresi üzerinde tanımlarlar. Bir küre yüzeyinde konum tespiti için de düzlemsel değil küresel trigonometri ilkelerinden faydalanılır. Küresel trigonometriyi düzlemsel trigonometri uygulamalarından ayıran en önemli özellik, üçgenin her bir kenarının birer yay parçası olması ve uzunluklarının açı birimiyle ifade edilmesidir. Küresel trigonometri uygulamadadüzlemsel trigonometriden farklıdır. Bu nedenle gökbilimsel problemlerin çözümü için kullanılan trigonometrik eşitlikler bazı temel farklılıklar içerir.
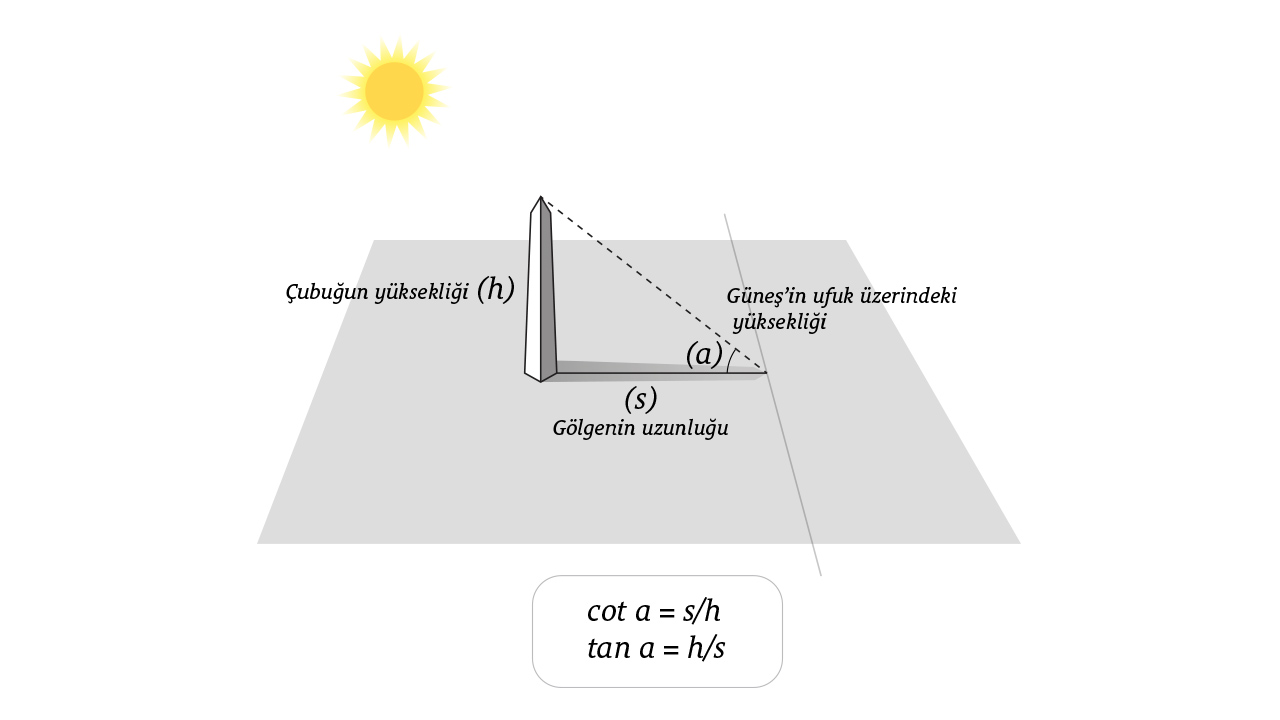
Tanjant (bir dik üçgende bir açının karşısındaki kenarın uzunluğunun komşusundaki kenarın uzunluğuna bölünmesiyle elde edilen oran, açının tanjantı olarak ifade edilir) ve kotanjant (bir dik üçgende bir açının komşusundaki kenarın uzunluğunun karşısındaki kenarın uzunluğuna bölünmesiyle elde edilen oran, açının kotanjantı olarak ifade edilir) fonksiyonları ise güneş saatleriyle zamanı tespit edebilmek için kullanıldı. Trigonometri alanında önemli çalışmalar yapan matematikçilerden biri olan Battanî, bir çubuğun yüksekliği ve gölgesinin uzunluğunun oranından Güneş’in ufuk üzerindeki yüksekliğini bulan bir yöntem geliştirdi. Bu nedenle Battanî tanjantı “uzamış gölge” olarak tanımlıyordu.
973 yılında bugün Türkmenistan ve Özbekistan sınırlarında kalan Harezm’de doğan Bîrunî, modern trigonometrinin temelini atan bilim insanlarından biri olarak kabul edilir. Bîrunî, Dünya’nın yarıçapını hesaplamak için trigonometriden yararlandı. İlk olarak düz ovada yükselen bir dağın yüksekliğini ölçmek için aralarındaki mesafe bilinen iki nokta ile dağın tepe noktası arasındaki açıları ölçtü. Bu verilerden trigonometrik hesaplamalar yoluyla dağın yüksekliğini hesapladı. Daha sonra dağın tepesine çıktı ve ufuk çizgisi ile arasındaki açıyı ölçtü. Bîrunî, bir köşesi dağın tepesinde, bir köşesi Dünya’nın merkezinde ve bir köşesi ufuk çizgisinde olan devasa bir üçgen hayal etti. Dağın yüksekliği ve dağın tepesi ile ufuk çizgisi arasındaki açı verilerini kullanarak Dünya’nın yarıçapını hesapladı.
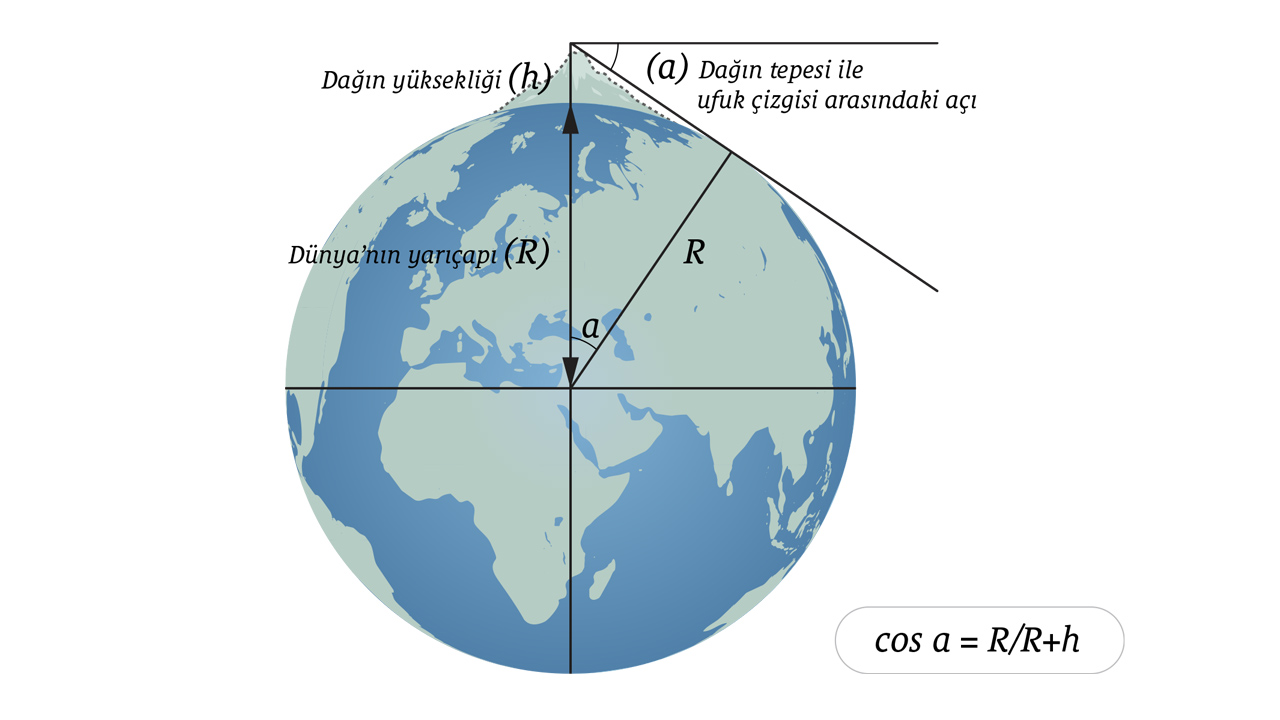
Bîrunî bu yöntemle Dünya’nın yarıçapını 6340 km olarak ölçtü. Bugün Dünya’nın tam olarak küre şeklinde olmadığını biliyoruz. Dünya’nın yarıçapı Ekvator bölgesinde yaklaşık 6378,14 km; kutup bölgelerinde 6356,75 km; Dünya’nın ortalama yarıçap değeri ise 6371 km. Yani günümüzden bin yıldan fazla zaman önce Bîrunî trigonometriyi kullanarak Dünya’nın yarıçapını %1’den daha az hatayla hesaplayabilmişti.
Kaynaklar:
- Sezgin, F., İslam Uygarlığında Astronomi, Coğrafya ve Denizcilik, Boyut Yayıncılık, İstanbul, 2018.
- 1001 İcat: Dünyamızda İslam Mirası, Ed.: Salim T S Al-Hassani, Foundation for Science Tecnology and Civilisation, 2010.
- https://nrich.maths.org/6843∂=
- https://muslimheritage.com/the-science-of-al-biruni/
- https://muslimheritage.com/muslim-founders-mathematics/
- http://blogs.nature.com/houseofwisdom/2012/09/remembering-al-biruni-the-first-anthropologist.html
