Antik Uygarlıklarda Matematik Sembolleri

Antik Uygarlıklarda Matematik Sembolleri

Antik Uygarlıklarda Matematik Sembolleri

Alışveriş yaparken, yemek pişirirken, otomobil kullanırken, problem çözerken ya da spor yaparken… Günlük hayatımızın birçok anında farkında olmasak da matematikten faydalanırız. Çok eski zamanlardan beri hesap yapmak için kullanılan matematikteki rakamlar farklı medeniyetler tarafından farklı sembollerle ifade edilmişti.

İnsanların yerleşik hayata geçmesiyle birlikte ticaretle uğraşmaya başlamaları ve tarım alanlarının hesaplanmasına ihtiyaç duymaları, matematiğin yazılı sembollerle ifade edilmesine neden oldu. İlk başlarda rakamlar doğa veya dünya ile ilişkili, kolay algılanabilecek sembollerle yazılıyordu: Örneğin 1 için Güneş, 2 için gözler ya da bir kuşun kanatları, 3 için yonca, 4 için hayvan ayakları kullanılıyordu.

Eski Mısır’da da rakamlar için resimli semboller tercih ediliyordu. Bu semboller çiçek, parmak, kurbağa gibi resimlerden ve çizgilerden oluşuyordu: Örneğin 1 rakamı dik bir çizgi şeklinde, 10 sayısı yay, 100 sayısı spiral ip, 1000 sayısı ise çiçek resmiyle ifade ediliyordu. 9 rakamı için dokuz çizgiyi ya da 3000 sayısı için üç çiçek sembolünü yan yana koymak gerekiyordu.

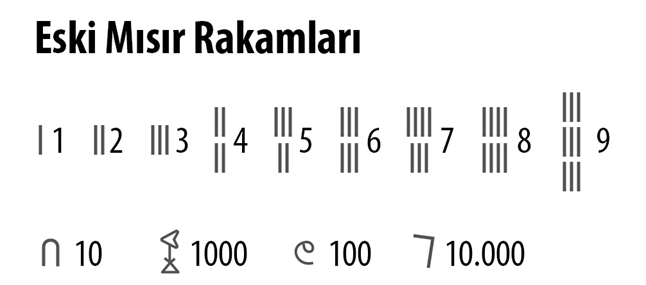
Antik Uygarlıklarda Matematik Sembolleri #1

Eski Mısırlılar, matematikte günümüzdeki gibi 10 tabanlı sayı sistemini kullanıyordu. Bu sayı sisteminin insan elindeki 10 parmaktan esinlenilerek oluşturulduğu düşünülüyor.

10 tabanlı sayı sisteminde sayılar 0’dan 9’a kadar rakamlardan oluşur. Bu rakamlar kullanılarak sayılar 10 ve katları şeklinde basamaklandırılır, sayı değeri bulunurken verilen sayının en soldaki rakamı, yanındaki basamak sayısınca 10 ile çarpılır.

Örneğin 12.345 sayısı

1×104+2×103+3×102+4×101+5×100

şeklinde yazılır. Yani 12.345 sayısındaki 1’in sayı değeri aslında 10.000’dir.

Babilliler ise matematikte 60 tabanlı sayı sistemini kullanıyordu. 60 tabanlı sayı sisteminin, 60 sayısının kendinden küçük bölenlerinin çok olması nedeniyle kesirli işlemlerin yapılmasını kolaylaştırdığı için tercih edildiği düşünülüyor. Örneğin bir günün 12’şer saatten gece ve gündüz olarak bölünmesi günlük işlerin planlanmasında kolaylık sağlıyor.

Babillilerin kullandığı matematik sisteminde toplamda 59 sembol vardı. Bu semboller ise sadece iki şekilden oluşuyordu. 1 rakamı çivi ile, 10 sayısı ise bir köşe çengeliyle resimlendiriliyordu.

Antik Uygarlıklarda Matematik Sembolleri #2

1 rakamını temsil eden çivi görseli ve 10 sayısını temsil eden köşe çengeli görseli

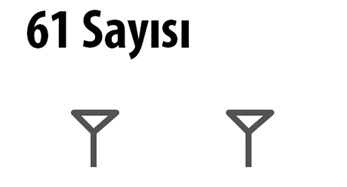
Babillilerin matematik sembollerinde 1 rakamını temsil eden görsel aynı zamanda 60 ve 60’ın katlarını da ifade ediyordu. Sembollerin yazılışlarındaki birbirine uzaklıkları ise sembolün hangi sayıyı temsil ettiğini gösteriyordu. Örneğin 61 sayısı birbirine belirli mesafede yan yana duran iki tane 1 rakamı yani iki tane çivi ile gösteriliyordu.

Antik Uygarlıklarda Matematik Sembolleri #3

Günümüzde 1 günü 24 saate, 1 saati 60 dakikaya, 1 dakikayı 60 saniyeye ya da 3600 saliseye bölmemiz veya çemberi 360° olarak ifade etmemiz 60 tabanlı sayı sistemine dayanıyor. Bu sayı sistemi hâlen denizcilik ve astronomide koordinat hesaplamalarında kullanılıyor.

Görseli büyütmek için üstüne tıklayın.

Antik Uygarlıklarda Matematik Sembolleri #4

Üzerinde matematik sembolleri bulunan Babil kil tableti

Mayalar ise matematikte 20 tabanlı sayı sistemini kullanıyordu. Yani 10 tabanlı sistemdeki gibi 1, 10, 100 veya 1000 yerine 1, 20, 400 ve 8000 sayılarıyla işlemleri gerçekleştiriyorlardı. Mayaların 20 tabanlı sayı sisteminin el ve ayak parmaklarının toplamından oluştuğu düşünülüyor. Toplamda 19 sayıdan oluşan bu sistemde sadece üç sembol bulunuyordu. Bu semboller 0’ı temsil eden deniz kabuğu şekli, 1’i temsil eden nokta ve 5’i temsil eden yatay çizgiden oluşuyordu. Mayalar 0’ı rakam olarak kullanan en eski medeniyetlerden biridir.

Antik Uygarlıklarda Matematik Sembolleri #5

1’den 19’a kadar olan sayıların Mayaların kullandığı matematik sembolleriyle ifade edilişi

Mayalar rakamları yazarken sembolleri yan yana değil aşağıdan yukarı doğru yerleştirirlerdi. Örneğin 18 sayısı için aşağıdan yukarıya üç tane 5 sembolü ve bunların üzerine üç tane 1 sembolü eklerlerdi. 20’den büyük sayıları yazarken Babilliler gibi sayıları sembollerin birbirlerine olan mesafeleriyle oluştururlardı. Sayının değerini en alttaki sayıyı 1 ile, onun üzerindeki sayıyı 20 ile çarparak hesaplarlardı. Örneğin 31 sayısını yazmak için 11 sayısını 1 ile, 1 sayısını ise 20 ile çarpar ve elde edilen değerleri toplayarak sayının gerçek değerini bulurlardı.

Rakamları ifade etmedeki farklılıklar günümüzde de mevcut. Birçok ülke matematikte rakamlar için 0, 1, 2, 3, 4,… gibi benzer semboller kullansa da Yunanistan, Suudi Arabistan ve Çin gibi bazı ülkeler rakamları kendi alfabelerindeki sembollerle ifade ediyor.

Kaynaklar:

Yorum yapın