9. Sınıf Matematik Ders Kitabı Meb Yayınları Sayfa 137 Alıştırmalar Soruları ve Cevaplarını yazımızın devamından okuyabilirsiniz.
ALIŞTIRMALAR
1. A = {(0,4), (1/2,3), (-1,5), (5,2/3), (3,2)} kümesinin elemanlarından kaç tanesinin 2x + 3y = 12 denklemini sağladığını bulunuz.
Parantez içinde verilen değerlerden ilki x,ikincisi y değeridir.Şimdi tek tek değerleri verip denklemde yerine koyup deneyelim ;
(0,4) için x=0,y=4 2.0+3.4=12 (sağladı)
(1/2,3) için x=1/2,y=3 2.1/2+3.3=10 (sağlamadı)
(-1,5) için x=-1,y=5 2.-1+3.5=13 (sağlamadı)
(5,2/3) için x=5,y=2/3 2.5+3.2/3=12 (sağladı)
(3,2) için x=3,y=2 2.3+3.2=12 (sağladı)
3 ifade denklemi sağlar.
2. Aşağıda verilen denklem sistemlerinin çözüm kümelerini bulunuz.
a) -5x + 3y = 22
2x – 3y = -16
b) 7a – 3b = 10
2a + 5b = -3
c) x/2 + y/3 = -1
2x/3 – y/2 = 10
ç) 1/(x+1) – 2y = -11
x/(x+1) + 4y = 22
a) y değerini yok edelim. Böylece x değerinin bulabiliriz.
-5x + 3y = 22
2x – 3y = -16
Bu iki denklemi alt alta toplarsak y değeri yok olacaktır.
-3x = 22-16 = 6
x = -2 olur.
x yerine -2 sayısını yazdığımızda y değerini buluruz.
10 + 3y = 22
3y = 12
y = 4 olur.
b) İki denklemi genişletmemiz gerekecek bu soruda. İlk denklemi 5 ile ikinci denklemi de 3 ile genişletirsek bilinmeyen bir değeri yok etmiş oluruz.
35a – 15b = 50
6a + 15b = -9
İki denklemi toplarız.
41a = 41
a = 1 buluruz.
İlk denklemde a yerine 1 yazıp b değerini bulalım.
7 – 3b = 10
– 3b = 3
b = -1 olur.
c) Her iki denklemi de tek bir paydada yazarak başlayalım işlemimizi yapmaya.
(3x + 2y)/6 = -1 yani;
3x + 2y = -6
(4x – 3y)/6 = 10 yani;
4x – 3y = 60
Yeni denklemlerimizi alt alta yazalım ve uygun sayılarla genişletelim. Yeni sayılarımızı toplayıp bilinmeyen değerlerimizi bulalım.
3x + 2y = -6
4x – 3y = 60
İlk denklem 3 ile ikinci denklem 2 ile genişletilir.
9x + 6y = -18
8x – 6y = 120
17x = 102
x = 6
Oluşturduğumuz denklemlerin birinde x yerine 6 yazalım ve y değerini bulalım.
18 + 2y = -6
2y = -24
y = -12
ç) Bu soruyu çözmek için biraz önceki yöntemlerden yararlanırsak işlemlerimiz çok uzar ve yorucu bir hal alır. Çok daha basit bir şekilde çözmek için sonuçları birbirine eşitleriz. İlk denklemimizin sonucu -11 ve ikinci denklemin sonucu 22’dir. İlk denklemi -2 ile çarparsak ikinci denklem ile eşit olur. Sonra da her iki denklemi birbiri ile eşitleriz.
-2 / (x + 1) +4y = x / (x+1) + 4y
Bu iki denklemde 4y değerleri birbirini götürür. x de karşı denklemde bulunan -2 sayısı ile eşittir. Bize soruda verilen denklemlerde x yerine -2 yazalım ve y değerini bulalım.
1 / (-2 + 1) – 2y = -11
-1 -2y = -11
-2y = -10
y = 5
3. 3x + 4y = 78 denkleminin çözüm kümesinin elemanlarından biri (a-1 , a+1) ise a değerini bulunuz.
Denklemin çözüm kümesi elemanları bize soruda verilmiş. x yerine a-1 ve y yerine a+1 yazarak işlemimizi yapalım.
3 (a – 1) + 4 (a + 1) = 78
3a – 3 + 4a + 4 = 78
7a +1 = 78
7a = 77
a = 11
4.- 2x + 5y = -3, (m – 2).x + 2y = n – 2 denklem sisteminin çözüm kümesi sonsuz elemanlı ise m.n değerini bulunuz.

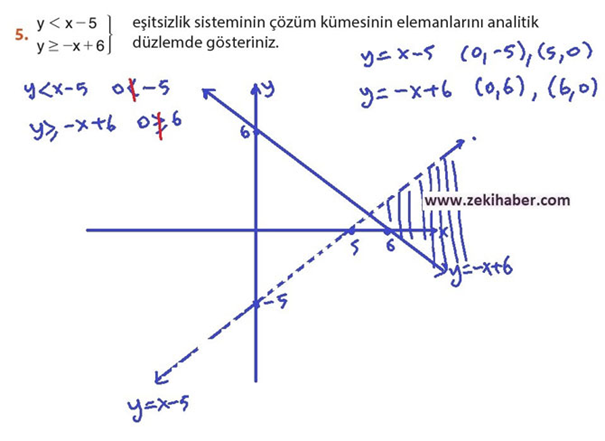
5. y < x – 5, y ≥ -x + 6 eşitsizlik sisteminin çözüm kümesinin elemanlarını analitik düzlemde gösteriniz.
6. Toplamları en çok 6, farkları en az -2 olan gerçek sayı ikililerini analitik düzlemde gösteriniz.
İki sayımızdan biri ” x ” diğeri ise ” y ”olsun.Verilenleri denklem kurarak çözelim.Toplamları en çok 6 demiş x+y = 6 deriz.Farkları en az x-y = -2 deriz.Taraf tarafa toplama yaparsak :
x+y= 6
x-y= -2
———–
2x = 4
x= 2 olur.Bulduğumuz değerini yerine yazalım :
2+y = 6
y= 4 olur.
7. -5x + y > 10, x ≤ -2 eşitsizlik sisteminin çözüm kümesini analitik düzlemde gösteriniz.
Soruda bize iki tane eşitsizlik sistemi verilmiş. İkinci eşitsizlik sayesinde x’in alabileceği değerleri görebiliriz.
İlk eşitsizlikte x yerine alabileceği en büyük değeri yazarak başlayalım.
x = -2 için
10+y>10
y>0
Bir sonraki en büyük tam sayıyı yazalım. Böylece eşitsizliği hangi y değeri sağlar bunu öğrenmiş olacağız.
x = -3
15+y>10
y>-5
Bu iki x değeri sayesinde anlarız ki x’in en büyük olduğu noktada y, 0’dan büyük bir sayıdır. x sayısı küçüldükçe y sayısı da küçülecektir. x sayısının sonsuza kadar küçüldüğünü de eşitsizlikte bize bir uç değer vermediğinden anlayabiliriz. Bu demek oluyor ki x sayısı sonsuza kadar küçülüyorsa, bu sayıya karşılık gelen y sayısı da sonsuza kadar küçülür.
Kısaca toparlayalım. Eşitsizlikte bize verilen x sayısı sonsuzdan gelip -2’de maksimum değeri alır. x sayısına karşılık gelen y değeri de sonsuzdan gelir 0’dan büyük bir değer alır.
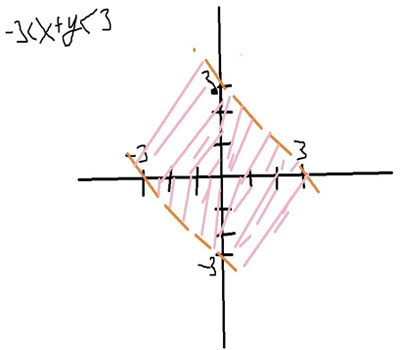
8. |x + y| < 3 eşitsizliğinin çözüm kümesini analitik düzlemde gösteriniz.
(a ∈ R+ , | x | < a ise -a < x < a olduğunu hatırlayınız. )
Doğruların denklemi yazdığında x+y nin her zaman -3 ten büyük 3 den küçük olduğu görülecektir.
x/3+y/3=1
-x/3+-y/3=1
Birinci denklemde 0,0 noktası sağlar çünkü 3 den küçük oluyor ondan aşağıyı boyadım.İkincide 0,0 yine sağladı ondan yukarı boyadım.