9. Sınıf Matematik Ders Kitabı Meb Yayınları Sayfa 120 Alıştırmalar Soruları ve Cevaplarını yazımızın devamından okuyabilirsiniz.
ALIŞTIRMALAR
1. -6 ∙ (2x + 4) + 4x = 8x + 40 denkleminin çözüm kümesini bulunuz.
Çözüm->
-12x – 24 + 4x = 8x + 40
-8x -8x = 40 + 24
-16x = 64
x = -4
2. 3x – 5 – [x + 6 – 2(9 + 3x)] = 0 denkleminin çözüm kümesini bulunuz.
Çözüm->
3x – 5 – [x + 6 – 2(9 + 3x)] = 0
3x – 5 – x – 6 + 18 + 6x = 0
8x + 7 = 0
8x = -7
x = -7/8
3. [(2x + a -5) / (ax – 7)] = x +1 / x – 1 denkleminin kökü 4 olduğuna göre a değerini bulunuz.
Çözüm ->
x’in yerine 4’ü yazalım
[(2x + a -5) / (ax – 7)] = x +1 / x – 1
(2.4 + a – 5 / a. 4 – 7) = 4 + 1 / 4 – 1
(8 + a – 5 / 4a – 7) = 5 / 3
(3 + a / 4a – 7) = 5 / 3
İçler dışlar çarpımı yapalım
20a – 35 = 9 + 3a
20a – 3a = 9 + 35
17a = 44
a = 44 / 17
4. m, n d R olmak üzere -m ∙ (2x – 6) + 6x – n = 0 denkleminin çözüm kümesinin tüm gerçek sayılar olabilmesi için m ve n değerlerini bulunuz.
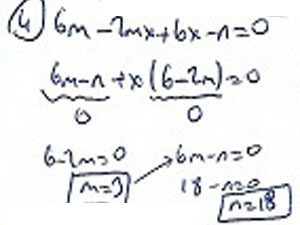
5. x E R olmak üzere -2 ≤ x – 4 / 3 < 4 ise x in değer aralığını bulup sayı doğrusu üzerinde gösteriniz.
Çözüm ->
-6 ≤ x – 4 < 12
-2 ≤ x < 16
<————– -2……………………….16 ———>
6. a d R olmak üzere -4 < a ≤ 5 eşitsizliği veriliyor. -3a + 7 ifadesinin alabileceği kaç farklı tam sayı değerinin olduğunu bulunuz.
Çözüm ->
– 15 ≤ -3a < 12
-8 ≤ 3a + 7 < 19
19 – (-8) = 27 tane
7. x, y E R olmak üzere
5 < x – 2 ≤ 9 -> 7 < x ≤ 11
-3 ≤ y + 3 ≤ 6 -> -6 ≤ y ≤ 3 -> -3 ≤ -y ≤ 6
eşitsizlikleri veriliyor. Aşağıdaki ifadelerin değer aralıklarını bulunuz.
a) x + y — > 1 < x + y ≤ 14
b) x – y –> 4 < x – y ≤ 17
c) x . y –> -66 ≤ x . y ≤ 33
ç) 2x – 3y
14 < 2x ≤ 22
-9 ≤ -3y ≤ 18
Toplayalım
5 < 2x – 3y ≤ 40
8. 3x – 6 ≤ 4x + 2 < 2x + 10 eşitsizliğini sağlayan x gerçek sayılarının alabileceği kaç farklı tam sayı değeri olduğunu bulunuz.

