9. Sınıf Matematik Ders Kitabı Meb Yayınları Sayfa 104, 105 Alıştırmalar Soruları ve Cevaplarını yazımızın devamından okuyabilirsiniz.
ALIŞTIRMALAR
1. 8’e , 12’ye ve 20’ye bölünebilen 600 den küçük, en büyük pozitif tam sayısını bulunuz.
8 e , 12 ye ve 20 ye bölünebilen sayıyı bulabilmek için bu sayıların en küçük ortak katını (ekok) bulmamız gerekir.
Ekoku dosyadaki şekilde bulabiliriz.
Gösterilen şekilde ekok 120 olarak bulunur.
600 den küçük denildiği için 120 nin 600 den küçük katlarına bakmalıyız.
120, 240, 360,480 ve 600 diye devam ederken 600 den küçük olarak en büyük 480 sayısı bulunur.
Cevap 480 dir.
8 12 20 | 2
4 6 10 | 2
2 3 5 | 2
1 3 5 | 3
1 5 | 5
1
120 x 4 = 480
2. 156 ve 442 sayılarını tam bölen en büyük doğal sayının rakamları toplamını bulunuz.
Ortak bölenler iki türlüdür.Ebob ve Ekok olmak üzere iki gruba ayrılır.Ebob demek ”b ” harfi ile en büyük böleni çağrıştırmaktadır.Ekok ise ” k ” harfi ile en küçük böleni çağrıştırmaktadır.
Ortak bölenlerini EBOB ile bulabiliriz.Ebob,her ikisininde ortak böleni olmasıdır.
442 156 / 2*
221 78 / 2
221 39 / 3
221 13/ 13*
17 1 /17
1
(156, 442) ebob = 2 . 13 = 26 Ebob ” 26 ” sayımızın rakamlarının toplamı : 2+6 =8 olur.
3. Bir çiçekçi güllerini üçerli, beşerli ve sekizerli saydığında her defasında 2 gül artmaktadır. Gül sayısı 200 den fazla olduğuna göre bu çiçekçinin en az kaç gülünün olduğunu bulunuz.
Soruyu çözebilmemiz için öncelikle 3, 5 ve 8 in en küçük ortak katını bulmamız gerekiyor. O halde:
3x5x8=120 (sayılar aralarında asal olduğu için direkt çarptık)
120 sayısı 3, 5 ve 8 ile tam bölünen en küçük sayıdır. Soruda 3, 5 ve 8 ile bölümünden kalanın 2 olması gerektiği verilmiş. O halde bu sayıya 2 ekleyelim:
120+2=122 ==> Güllerin 200’den fazla olması gerekiyor. 122 sayısına 120 eklersek hem güller 200 den fazla olur hem de 3, 5 ve 8 ile bölümünden 2 kalma şartı korunmuş olur. O halde:
122+120=242
Çiçekçinin en az 242 gülü vardır.
4. a, b, c sayıları birer doğal sayıdır. K = 3a + 1 = 4b + 2 = 5c + 3 olduğuna göre K nin en küçük değerini bulunuz.

5. Boyları 120 cm, 135 cm ve 180 cm olan üç demir çubuk eşit büyüklükte ve artmayacak şekilde parçalara ayrılacaktır. Bu iş için en az kaç kesim yapılması gerektiğini bulunuz (Çubuklar ayrı ayrı kesilecektir).
büyük parçalardan küçük parçalara bölünme işlemi olduğu için ebob sorusudur (120,135,180)ebob=
120 135 180 | 2
60 135 90 | 2
30 135 45 | 2
15 135 45| 3 +
5 45 15 | 3
5 15 5 | 3
5 5 5 | 5 +
1 1 1 ise EBOB(120,135,180)=15 deriz
çubuklar ayrı ayrı kesilecek ise hepsine ayrı işlem yapılmalıdır.
1. ÇUBUK (120)
120/15 = 8 8 PARÇAYI KESMEK İÇİN 7 KESİM YAPILIR
2. ÇUBUK (135)
135/15 = 9 9 PARÇAYI KESMEK İÇİN 8 KESİM YAPILIR
3. ÇUBUK (180)
180/15 = 12 12 PARÇAYI KESMEK İÇİN 11 KESİM YAPILIR
7+8+11= 26 kesim yapılır.
6. Boyutları 4 cm, 5 cm ve 6 cm olan dikdörtgenler prizmasından en az kaç tanesi yan yana ve üst üste getirilirse bir küp oluşur? Bulunuz.
Öncelikle küp oluşturmak için bütün kenarların eşit olması gerekiyor. En az dikdörtgen prizma kullanarak dediği için:
4, 5 ve 6 nın en küçük ortak katını bulmamız gerekiyor:
4 5 ve 6 ‘nın en küçük ortak katı 60’tır. O halde:
60/4=15
60/5=12
60/6=10
10+12+15=37 tane kullanarak bir küp oluşturabiliriz.
7. A, B, C firmaları Yozgat İstanbul arasında sırasıyla 3 günde, 4 günde ve 5 günde bir sefer düzenliyor. Bu firmalar birlikte ilk seferlerine başladıktan kaç gün sonra 2. kez birlikte tekrar sefere çıkacaklarını bulunuz.
EKOK(3,4,5) = 60
1. kez 60 gün sonra
2. kez 120 gün sonra birlikte sefere çıkarlar
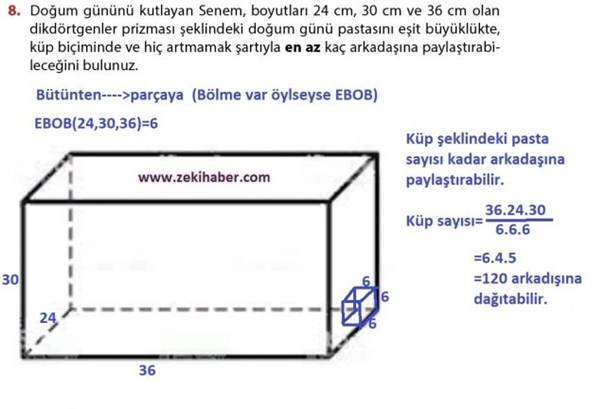
8. Doğum gününü kutlayan Senem, boyutları 24 cm, 30 cm ve 36 cm olan dikdörtgenler prizması şeklindeki doğum günü pastasını eşit büyüklükte, küp biçiminde ve hiç artmamak şartıyla en az kaç arkadaşına paylaştırabileceğini
bulunuz.
9. Yukarıda verilen asal çarpanlara ayırma algoritmasında A + B + C toplamını bulunuz.

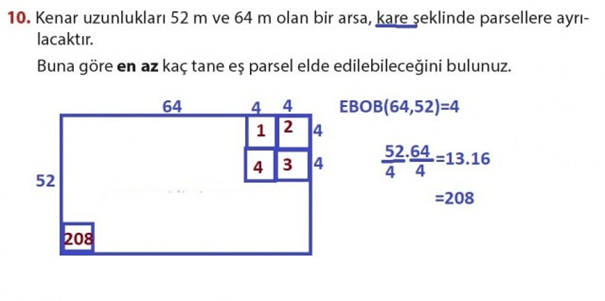
10. Kenar uzunlukları 52 m ve 64 m olan bir arsa, kare şeklinde parsellere ayrılacaktır. Buna göre en az kaç tane eş parsel elde edilebileceğini bulunuz.
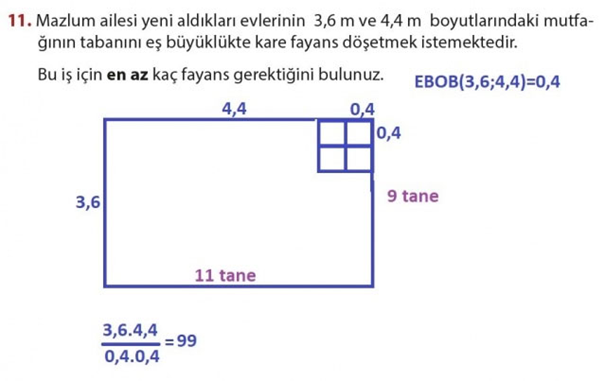
11. Mazlum ailesi yeni aldıkları evlerinin 3,6 m ve 4,4 m boyutlarındaki mutfağının tabanını eş büyüklükte kare fayans döşetmek istemektedir. Bu iş için en az kaç fayans gerektiğini bulunuz.
12. Sinem; bahçelerindeki ağaçları üçerli saydığında 1, beşerli saydığında 3, yedişerli saydığında 5 ağaç artmaktadır. Buna göre bahçede en az kaç ağaç olduğunu bulunuz.

