10. Sınıf Meb Yayınları Matematik Fonksiyonlar Sayfa 94 Alıştırmalar Cevaplarını yazımızın devamından okuyabilirsiniz.
ALIŞTIRMALAR
1. Aşağıdaki ifadelerin tanımlı olduğu aralıklarda fonksiyon olup olmadıklarını bulunuz.

2. f : A -> R bir fonksiyon,
A = {-3, – 1, 0, 1, 3} ve f(x) = 5x + 4 olduğuna göre bu fonksiyonun görüntü kümesini bulunuz.
Sonuçların kümesi f(A)
f(-3) = -15 + 4 = – 11
f(-1) = -5 + 4 = -1
f(0) = 4
f(1) = 9
f(3) = 19
f(A) = {-11, -1, 4, 9, 19}
3. Bir f : A -> R fonksiyonu “Her x gerçek sayısını kendisinin karesinin 5 eksiği ile eşleştirmektedir.’’ şeklinde tanımlanmıştır.
Buna göre f fonksiyonu için // x –> x2 – 5
a) 7 nin görüntüsünü bulunuz. // f(7) = 72 – 5 = 44
b) f(-3) ifadesinin değerini bulunuz. // f(-3) = (-3)2 – 5 = 4
c) Görüntüsü 4 olan sayıları bulunuz.
x2 – 5 = 4
x2 = 9
x1 = 3 x2 = -3 {3, -3}
4. f : A ” B bir fonksiyon,
f(A) = {5, 7, 11, 19} ve f(x) = 2x – 9 olduğuna göre bu fonksiyonun tanım kümesini bulunuz.
2x – 9 = 5
2x = 14
x1 = 7
2x – 9 = 7
2x = 16
x2 = 8
2x – 9 = 11
2x = 20
x = 10
2x – 9 = 19
2x = 28
x = 14
A = {7, 8, 10, 14}
5. f : R ” R, f(x + 2) = 3x – 4 olduğuna göre aşağıdaki ifadelerin değerlerini bulunuz.
a) f(5) –>
f(x + 2) = 3x – 4
x + 2 = 5
x = 3
f(5) = 3 . 3 – 4
f(5) = 5
b) f(1)
x + 2 = 1
x = -1
f(1) = 3 . (-1) – 4
f(1) = -7
c) f(x + 5)
f(x + 2) = 3x – 4
(x + 3) (x + 3)
f(x + 5) = 3(x + 3) – 4
f(x + 5) = 3x + 5
ç) f(2x + 1)
f(x + 2) = 3x – 4
(2x-1) (2x-1)
f(2x + 1) = 3 . (2x -1) – 4
f(2x + 1) = 6x -7
6. f : R ” R olmak üzere f(x) = 3x + 7 ve f(a + 1) = 19 olduğuna göre a nın hangi sayıya eşit olduğunu bulunuz.
f(x) = 3x + 7
(x) –> Buraya geleni 3 ile çarp ve 7 ekle
f(a + 1) = 3 . (a + 1) + 7 = 19
3a + 10 = 19
3a = 9
a = 3
7. Aşağıdaki fonksiyonların bire bir fonksiyon olup olmadığını bulunuz.
a) f : R ” R, f(x) = 1 – x
x1 = x2
1 – x1 = 1 – x2
f(x1) = f(x2) => f ; 1:1 ‘dir
b) f : R ” R, f(x) = x2 + x
f(x) = x (x + 1)
Farklı sayıların kendisi ve bir fazlasının çarpımıda farklı olur. Bu nedenle f, 1:1 dir.
Örneğin 1 ≠ -1
f(1) = 1 + 1 = 2
f(-1) = 1 – 1 = 0
f(1) ≠ f(-1)
c) f : R ” R, f(x) = x3 – x
ç) f : R+ ” R, f(x) = x2 + 3

8. Aşağıdaki fonksiyonların örten ya da içine fonksiyon olup olmadığını bulunuz.
a) g : R -> R, g(x) = 5x + 2
b) g : R -> R, g(x) = 2×2 + 4
c) g : N -> Z, g(x) = 7 – 2x
ç) g : (-2, 8) -> R, g(x) = x + 2


9. f : R ” R, f(x + 1) – f(x) = 3x ve f(3) = 4 olduğuna göre f(1) ifadesinin değerini bulunuz.

10. f : R ” R, f(x2 + x – 1) = 3×2 + 3x – 8 olduğu na göre f(11) ifadesinin değerini bulunuz.

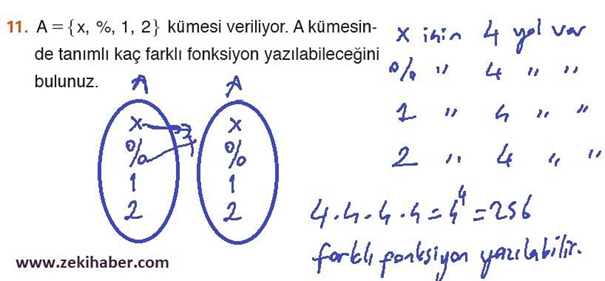
11. A = “x, %, 1, 2, kümesi veriliyor. A kümesinde tanımlı kaç farklı fonksiyon yazılabileceğini bulunuz.
12. f : R -> R, f(x) = 3x – 2 olduğuna göre f(x – 2) yi f(x)cinsinden bulunuz.

13. f : R -> R, f(x) = 32x-1 – ise f(x+1)/f(x-1) ifadesinin değerini bulunuz.

Not : Bu sayfadaki bazı soruların cevapları zekihaber.com sitesinden alınmıştır.
Cevap Anahtarı : 1. a) Fonksiyon b) Fonksiyon c) Fonksiyon değil ç) Fonksiyon değil
2. {-11, – 1, 4, 9, 19} 3. a) 44 b) 4 c) -3 ve 3 4. {7, 8, 10, 14}
5. a) 5 b) -7 c) 3x + 5 ç. 6x – 7 6. 3
7. a) Birebir b) Birebir değil c) Birebir değil ç) Birebir
8. a) Örten b) İçine c) İçine ç) İçine 9. -5 10. 28 11. 256 12. f(x)-6 13. 81
