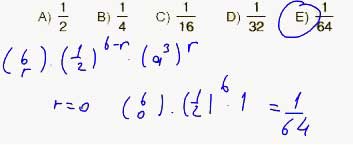10. Sınıf Matematik Ders Kitabı Sayfa 38-39 Cevapları Miray Yayınları
Konu Değerlendirme Soruları
1. Aşağıdaki ifadeler doğruysa boş kutulara ” D ” , yanlışsa ” Y ” yazınız.
(D) a. P ( n , r ) = C ( n, r ) eşitliği bazen doğrudur.
(Y) b. Kombinasyonda sıra önemliyken permütasyonda sıra önemli değildir.
(Y) c. Herhangi üçü doğrusal olmayan 8 noktadan P ( 8, 2 ) = 56 doğru geçer.
(D) ç. Herhangi üçü doğrusal olmayan 10 nokta ile C ( 10, 3 ) = 120 üçgen çizilebilir.
2. Aşağıda sol sütunda verilenlerin kaç farklı şekilde yapılabileceğini bulmak için permütasyon veya kombinasyondan hangisinin kullanılması gerektiğini belirleyip cevapları sağdaki sütundan bularak eşleştiriniz.
I. 9 farklı malzemeden 3’ünü seçerek pizza sipariş etmek (c. 84)
II. Bir mağazada ödeme yapmak için 4 kişinin sıraya girmesi (ç. 24)
III. TÜRKİYE sözcüğündeki harflerin tümünü kullanarak bir harf dizilimi oluşturmak (a. 5040)
IV. Bir iş yerinde çalışan 21 kişi arasından 4’ünü eğitim için yurt dışına göndermek (b. 5985)
3. Sonucu, P ( 7, 3 ) ve C ( 7, 3 ) olan iki problem yazınız.
Problem 1 – Permütasyon (P): Bir şirketin yönetim kurulu, 7 üyeden oluşmaktadır. Başkan, başkan yardımcısı ve sekreter pozisyonları için adaylar arasından seçim yapılacaktır. Kaç farklı şekilde bu üç pozisyon doldurulabilir?
Çözüm: P(7, 3) kullanarak çözebiliriz. Sonuç 210 olacaktır.
Problem 2 – Kombinasyon (C): Bir grup öğrenci arasından, bir matematik yarışması için 3 öğrenci seçilmesi gerekiyor. Toplamda 7 öğrenci başvurdu. Kaç farklı şekilde bu 3 öğrenci seçilebilir?
Çözüm: C(7, 3) kullanarak çözebiliriz. Sonuç 35 olacaktır.
4. Aşağıdaki eşitliklerin her birinde n’nin değerini bulunuz.
a. C ( n, 2 ) = 28 –> n = 8
b. (n / n – 1) = 6 –> (n 1) = 6 –> n = 6
c. (n 3) + (n 2) = 5n /2
ç. C ( n, 2 ) + P ( n, 2 ) = 30

5. 8 kız, 10 erkek arasından, 3’ü kız, 4’ü erkek 7 kişilik kaç değişik grup oluşturulabilir?
(8 3) . (10 4)
6. 8 elemanlı alt küme sayısı, 5 elemanlı alt küme sayısına eşit olan kümenin 2 elemanlı kaç alt kümesi vardır?
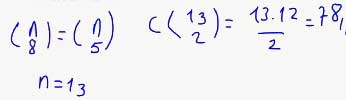
7. En çok 2 elemanlı, 29 tane alt kümesi olan bir küme kaç elemanlıdır?

8. 12 kişilik bir sporcu grubundan 6 kişilik bir takım oluşturulacaktır.
Takıma girecek 2 kişi belli olduğuna göre kaç değişik takım oluşturulabilir?
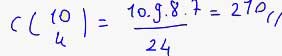
9. Herhangi üçü doğrusal olmayan 9 nokta ile birer köşeleri ortak olan kaç üçgen çizilebilir?
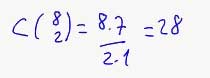
10. 10 kişilik bir gruptan, 3 kişilik bir temsilci grubu ve bu üç kişi içinden 1 başkan kaç farklı şekilde seçilebilir?
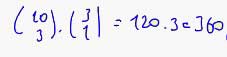
11. Bir sınavda sorulan 8 sorunun ilk 4’ünden en az 3’ünü cevaplamak koşuluyla 5 soru kaç değişik biçimde cevaplanabilir?
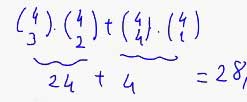
12. Bir çember üzerindeki 12 nokta ile kaç dörtgen çizilebilir?
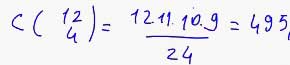
13. Yukarıda Pascal üçgeninden bir kesit verilmiştir. Verilen sayıları kullanarak boşlukları tamamlayınız.

14. Aşağıdaki noktalı yerleri uygun şekilde doldurunuz.
a. ( 2x + 3y ) n ifadesinin açılımında n + 1 tane terim vardır. Her terimde x ve y’nin üstleri
toplamı n
b. ( a + b ) n ifadesinin x’in azalan kuvvetlerine göre açılımındaki baştan 3. terim 28a 6b2
ise n = (8 2) = 28 –> n = 8
c. Pascal üçgeninin 8. satırında 8 tane terim vardır.
15. Bir ayrıtının uzunluğu ( 3x + 5 ) birim olan küpün hacmini veren açık bir ifade yazınız.
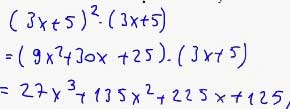
16. Aşağıda sol sütunda verilen ifadelerin eşitlerini sağ sütundan bularak eşleştiriniz ( Verilen ifadelerin açılımlarının x’in azalan kuvvetlerine göre düzenlendiğini varsayınız. ).
I. ( x – 2y ) 8 ifadesinin açılımındaki baştan 3. terim
II. ( 2x 2 – y ) 6 ifadesinin açılımındaki baştan 4. terim
III. (3y – x 6 ifadesinin açılımındaki baştan 4. terim

17. (r 3 – 2 / r 2 ) 30 ifadesinin açılımında, terimlerin r’nin azalan kuvvetlerine göre sıralanacağını kabul ederek;
a. Baştan 7. terimi bulunuz.
b. Sabit terimi bulunuz.

18. (1 / 2 + a 3 ) 6 ifadesinin açılımında sabit terim aşağıdakilerden hangisidir?
A) 1/2 B) 1/4 C) 1/16 D) 1/32 E) 1/64