
1. A = { 1, 2, 3 } , B = { 2, 4, 6 } olmak üzere A ” B ye tanımlanan aşağıdaki ilişkilerden hangileri
fonksiyondur?
a. f 1 = { ( 1, 6 ), ( 2, 6 ), ( 3, 6 ) }
b. f 2 = { ( 2, 1 ), ( 4, 2 ), ( 6, 3 ) }
c. f 3 = { ( 1, 2 ), ( 1, 4 ), ( 1, 6 ) }
d. f 4 = { ( 2, 2 ), ( 2, 4 ), ( 2, 6 ) }

2. f ( x ) = | x – 3 | + 4 ve h ( x ) = x 3 – x + 1 fonksiyonu
için f ( 1 ) ve h ( – 1 ) değerlerini bulunuz.

3. Aşağıdaki fonksiyonların tanım kümelerini bulunuz.

4. R de tanımlı

5. f : R ” R , f ( x ) = ( k + 2 ) . x – m + 4 fonksiyonu
birim fonksiyondur. Buna göre f ( m + k ) kaçtır?

6. f ( x ) = ( a – 3 ) x + 4 fonksiyonu sabit fonksiyon
olduğuna göre f ( a ) kaçtır?

7. f : R ” R , f bir doğrusal fonksiyondur. f ( 1 ) = 4 ve f ( – 2 ) = – 2 olduğuna göre f ( 3 ) kaçtır?

8. Z de tanımlı aşağıdaki fonksiyonlardan hangileri bire birdir?
a. f ( x ) = x + 2 b. g ( x ) = x 2

9. Z de tanımlı aşağıdaki fonksiyonlardan hangileri içinedir?
a. f ( x ) = 2x + 1 b. g ( x ) = x – 2

10. Aşağıda boş bırakılan yerlere “ tek ” ya da “ çift ” kelimelerinden uygun olanı yazınız.
a. f ( –x ) = –f ( x ) ise f fonksiyonu …………………. fonksiyondur.
b. Grafiği y eksenine göre simetrik olan bir fonksiyon …………………… fonksiyondur.
c. Bütün sabit fonksiyonlar ……………………….. fonksiyondur.
d. f ( x ) = x 2 + 1 fonksiyonu …………………. fonksiyon değildir.

11. f ( x ) fonksiyonunun grafiği y eksenine göre simetriktir.
f ( –x ) + 4x 4 = 6 x 2 – f ( x ) + 2 olduğuna
göre f ( –1 ) kaçtır?

12. f ( x ) = ( 4a – 8 ) x 5 – ( 3b + 12 ) x 2 + a – 6 fonksiyonu
tek fonksiyon ise a + b toplamı kaçtır?
A) –2 B) –1 C) 0 D) 1 E) 2

13. A = { 1, 2, 3, 4 } , B = { –1, –2, –3, –4 } ve
f : A → B, g : A → B olmak üzere,
f : { ( 1, –1 ), ( 2, –2 ) , ( 3, –3 ) , ( 4, –4 ) }
g : { ( 1, –4 ), ( 2, –3 ) , ( 3, –2 ) , ( 4, –1 ) }
olduğuna göre aşağıda istenen fonksiyonların kurallarını bulunuz.

14. R de tanımlı, f ve g fonksiyonları için,
f ( x ) = 2 – x ve
( 2g – f ) ( x ) = 5 x – 2
olduğuna göre g ( 2 ) aşağıdakilerden hangisidir?
A) 2 B) 4 C) 8 D) 10 E) 12

15. R de tanımlı, f ve h fonksiyonları için,
f ( x ) = 3 x + 1 ve
h ( x ) = x 2 – 1
olduğuna göre ( foh ) ( –1 ) değeri kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5

16. f : R → R , olmak üzere,
f ( x ) = 3x + m ve
( fof ) ( x ) = 9x + 8
olduğuna göre m değeri kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5

17. R de tanımlı, f ve k fonksiyonları için,

18. R de tanımlı, f ve k fonksiyonları için,
f ( x ) = 3x – 1 ve
( fok ) ( x ) = 4x + 5
olduğuna göre k ( x ) i bulunuz.

19. Gerçek sayılar kümesinde tanımlı f , k ve h fonksiyonları için aşağıdaki istenenleri bulunuz.

19. Gerçek sayılar kümesinde tanımlı f , k ve h fonksiyonları için aşağıdaki istenenleri bulunuz.

19. Gerçek sayılar kümesinde tanımlı f , k ve h fonksiyonları için aşağıdaki istenenleri bulunuz.


20. Aşağıdaki fonksiyonların, tanımlı oldukları aralıklardaki
terslerini bulup eşleştiriniz.

21. Gerçek sayılarda tanımlı f fonksiyonu için,

22. R de tanımlı, h ve g fonksiyonları için,
( h –1 o g ) ( x ) = 2x + 7 ve
g ( x ) = 3x + 1
olduğuna göre h ( x ) i bulunuz.

23. R de tanımlı, f ve k fonksiyonları için,
f ( x ) = 4x + 3 ve
k –1 ( x ) = 2x – 5
olduğuna göre ( f –1 o k ) –1 ( x ) i bulunuz.

24. R de tanımlı, h ve g fonksiyonları için,
g ( x ) = 3x – 1 ve
( g –1 o h ) ( x ) = 2x + 7
olduğuna göre h ( x ) i bulunuz.

25. R – { 2 } → R – { 2 } , f ( x ) =
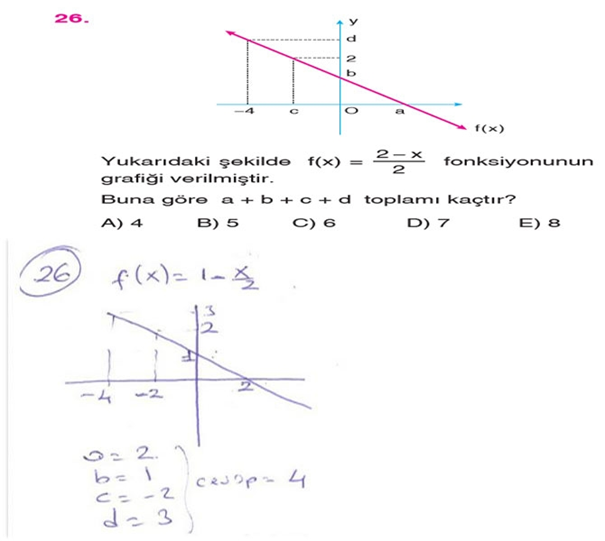
26. Yukarıdaki şekilde f(x) = 2 – x / 2 fonksiyonunun grafiği verilmiştir.
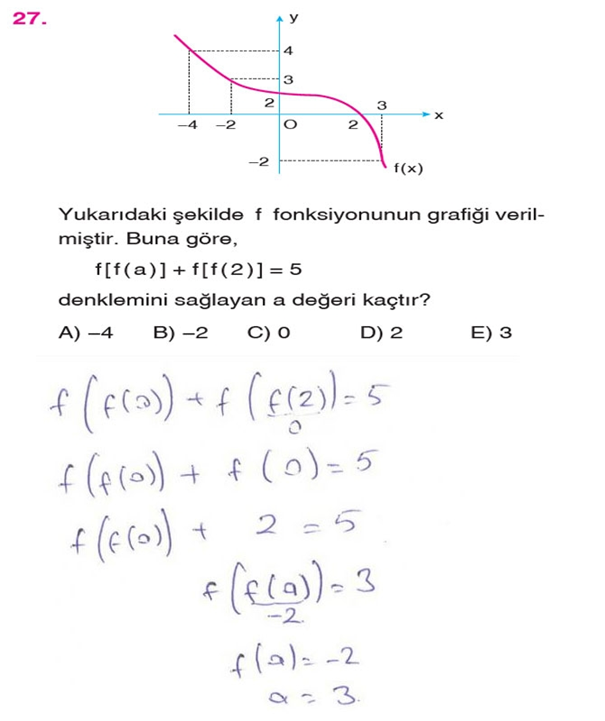
27. Yukarıdaki şekilde f fonksiyonunun grafiği verilmiştir.
Buna göre,
f [ f ( a ) ] + f [ f ( 2 ) ] = 5
denklemini sağlayan a değeri kaçtır?
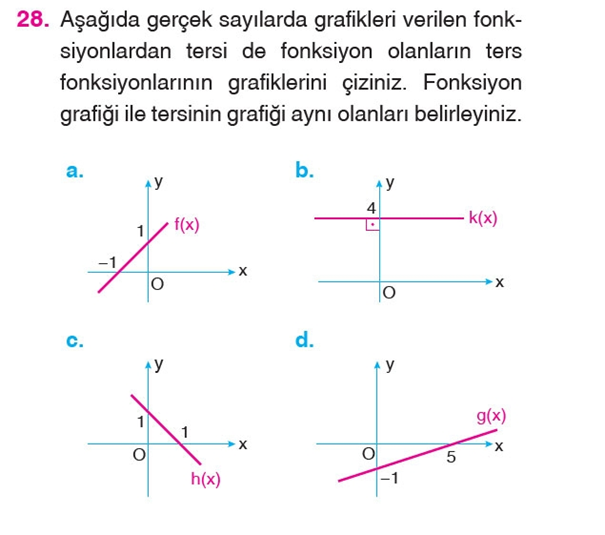
28. Aşağıda gerçek sayılarda grafikleri verilen fonksiyonlardan tersi de fonksiyon olanların ters
fonksiyonlarının grafiklerini çiziniz. Fonksiyon grafiği ile tersinin grafiği aynı olanları belirleyiniz.

28. Aşağıda gerçek sayılarda grafikleri verilen fonksiyonlardan tersi de fonksiyon olanların ters
fonksiyonlarının grafiklerini çiziniz. Fonksiyon grafiği ile tersinin grafiği aynı olanları belirleyiniz.

29. fonksiyonu veriliyor.
Buna göre a + b toplamı kaçtır?
A) –1 B) 0 C) 1 D) 2 E) 3
